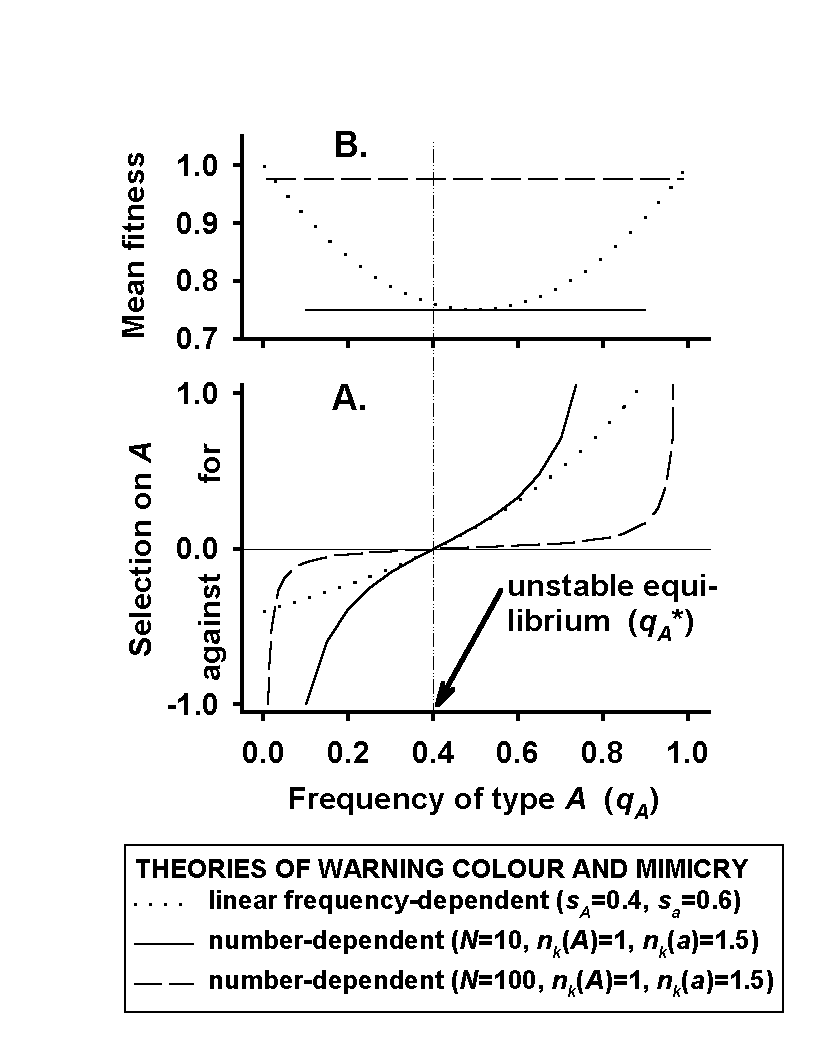
Müller's number-dependent theory supposes that, while they learn to avoid the pattern of an unpalatable insect, predators kill a constant number, n_k(i) of each morph i per unit time in a given area. Assuming the local population has constant size (N) and contains a novel pattern (A) and a "wild-type" pattern (a), Müller's theory can give the strength of frequency-dependent selection for or against the pattern A at different frequencies (q_A) in the population. The fitness of A is W_A = 1 - (n_k(A)/q_AN), while that of a is W_a = 1 - [n_k(a)/(1-q_A)N]. The measure of frequency-dependent selection acting on A relative to a used here is S_A = (W_A/W_a) - 1; if S_A is positive, A is favored, if S_A is negative, A is disfavored. The dashed and solid lines show the frequency-dependence for a low total population size (N = 10) and a high total population size (N = 100), respectively, relative to n_k(A) and n_k(a) (the fractions n_k/N are important, rather than absolute values of n_k and N). In contrast, linear frequency-dependent selection has been more normally used to study the population genetics of warning color and mimicry (37, 47, 54, 91, 93), for example where W_A = 1 - s_A(1 - q_A), and W_a = 1 - s_aq_A. This model gives the frequency-dependence shown in the dotted curve of the figure. In both number-dependent and frequency-depenedent selection, values of s and n_k have been chosen to give an unstable equilibrium frequency of q_A* = 0.4, which could be the case if A has 1.5× greater fitness than a.